JAVA字符串相似度算法
时间:2019-11-30 23:37:39|栏目:|点击: 次
字符串相似度算法
1. 介绍
最近项目中有一个小算法要求判断字符串大致内容相等,相当于模糊查询,正好查到了这个字符串相似算法。这个算法又被称为“编辑距离算法”,所谓编辑距离,就是用来计算从原串(s)转换到目标串(t)所需要的最少的插入,删除和替换的数目。
2.算法原理
这里,每一个格子是这样的
每一个格子由他的左边的格子上边的格子和左上角的格子决定。
具体来说,每一个方框的数字可以这样得来:
1. 左边的数字加一
2. 上边的数字加一
3. 如果这一格对应的行和列字母不同的话, 左上角的数字加一,否则加零。
c2处得来的:1+1=2
b3处得来的:1+1=2
b2处得来的:因为a与a相同,所以0+0 = 0;
在这三个书中,我们找最小的数,即0填入即可。
看到这,恐怕很多看官很奇怪了,没事干为啥加一加零的,凭啥就左上角的数要分情况?不要急,我们在看一个例子,有了这个例子我想回更好理解。
c3框的0加一得到1
b2框的2加一得到3
这次因为a和b不同,因此左上角(b3)得到的数为:1+1=2
同样,取最小的数为1。
下面我将说一下我对表中每一个框算法的理解,可能并不准确,希望能有助于大家理解:
以计算c4为例,我们给c3+1,其实相当于在比较a和ab两个字符串,想让这两个字符串相等,唯一的方法就是加一个b字符,因此要加一。但是,有人可能要问了:
那为什么我们从b4算c4的时候是2+1呢,ab到a不应该是去掉一个b吗?那不应该是1吗?
这个问题是这样的,在这个算法中,无论字符串是什么,表中第一行和第一列(例如本例中1行和b列),他都是从0写到字符串长度,我是这样理解的,他这里是这样算的,我们将ab删掉需要两步,再添加一个a需要一步,这里不要将a和ab代入,你就想像他是yz和x,这样就可以理解了。
(这里你去观察,其实上面的加一和左面的加一是两个字符串互相变化最笨的方法,即删掉本身在加上对方,如果我们单单看从c2到c4,我们把它看成x到yz,其实应该为1+1+1也是3。这也是为什么左边和上边的算法不用考虑相不相同的原因,低头黑加就行了(手动滑稽),真正引起里面数字变化的,是左上角的那个判断,也正因为有左上角的参加,这里的由a3到a4变成了1)
再次声明,上面只是我的个人理解,并不完全保证正确。
好了下面你只需要把这个表填完:
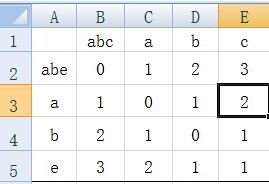
然后我们就会发现:从abc到abe需要一步。
最后:先取两个字符串长度的最大值maxLen,用1-(需要操作数除maxLen),得到相似度。
例如本题,abc 和abe 需要一个操作,长度为3,所以相似度为1-1/3=0.666。
1. 介绍
最近项目中有一个小算法要求判断字符串大致内容相等,相当于模糊查询,正好查到了这个字符串相似算法。这个算法又被称为“编辑距离算法”,所谓编辑距离,就是用来计算从原串(s)转换到目标串(t)所需要的最少的插入,删除和替换的数目。
2.算法原理
这里,我们举一个简单的例子,计算字符串“abc”“abe”的相似度。首先,需要构建一个二维数组,用来算最大编辑距离。如图:
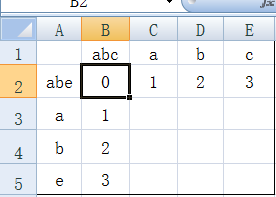
这里,每一个格子是这样的
每一个格子由他的左边的格子上边的格子和左上角的格子决定。
具体来说,每一个方框的数字可以这样得来:
1. 左边的数字加一
2. 上边的数字加一
3. 如果这一格对应的行和列字母不同的话, 左上角的数字加一,否则加零。
举个例子,我们现在填如图选定的那个框(c3)。
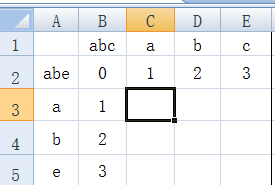
c2处得来的:1+1=2
b3处得来的:1+1=2
b2处得来的:因为a与a相同,所以0+0 = 0;
在这三个书中,我们找最小的数,即0填入即可。
看到这,恐怕很多看官很奇怪了,没事干为啥加一加零的,凭啥就左上角的数要分情况?不要急,我们在看一个例子,有了这个例子我想回更好理解。
这次我们填c4:
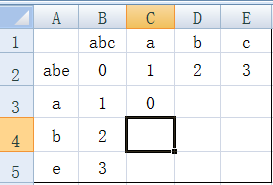
c3框的0加一得到1
b2框的2加一得到3
这次因为a和b不同,因此左上角(b3)得到的数为:1+1=2
同样,取最小的数为1。
下面我将说一下我对表中每一个框算法的理解,可能并不准确,希望能有助于大家理解:
以计算c4为例,我们给c3+1,其实相当于在比较a和ab两个字符串,想让这两个字符串相等,唯一的方法就是加一个b字符,因此要加一。但是,有人可能要问了:
那为什么我们从b4算c4的时候是2+1呢,ab到a不应该是去掉一个b吗?那不应该是1吗?
这个问题是这样的,在这个算法中,无论字符串是什么,表中第一行和第一列(例如本例中1行和b列),他都是从0写到字符串长度,我是这样理解的,他这里是这样算的,我们将ab删掉需要两步,再添加一个a需要一步,这里不要将a和ab代入,你就想像他是yz和x,这样就可以理解了。
(这里你去观察,其实上面的加一和左面的加一是两个字符串互相变化最笨的方法,即删掉本身在加上对方,如果我们单单看从c2到c4,我们把它看成x到yz,其实应该为1+1+1也是3。这也是为什么左边和上边的算法不用考虑相不相同的原因,低头黑加就行了(手动滑稽),真正引起里面数字变化的,是左上角的那个判断,也正因为有左上角的参加,这里的由a3到a4变成了1)
再次声明,上面只是我的个人理解,并不完全保证正确。
好了下面你只需要把这个表填完:

然后我们就会发现:从abc到abe需要一步。
最后:先取两个字符串长度的最大值maxLen,用1-(需要操作数除maxLen),得到相似度。
例如本题,abc 和abe 需要一个操作,长度为3,所以相似度为1-1/3=0.666。
ok!大功告成。下面是Java代码,有兴趣的可以直接复制粘贴去运行一下!
代码如下:
package code;
public class MyLevenshtein {
public static void main(String[] args) {
//要比较的两个字符串
String str1 = "今天星期四";
String str2 = "今天是星期五";
levenshtein(str1,str2);
}
public static void levenshtein(String str1,String str2) {
//计算两个字符串的长度。
int len1 = str1.length();
int len2 = str2.length();
//建立上面说的数组,比字符长度大一个空间
int[][] dif = new int[len1 + 1][len2 + 1];
//赋初值,步骤B。
for (int a = 0; a <= len1; a++) {
dif[a][0] = a;
}
for (int a = 0; a <= len2; a++) {
dif[0][a] = a;
}
//计算两个字符是否一样,计算左上的值
int temp;
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
temp = 0;
} else {
temp = 1;
}
//取三个值中最小的
dif[i][j] = min(dif[i - 1][j - 1] + temp, dif[i][j - 1] + 1,
dif[i - 1][j] + 1);
}
}
System.out.println("字符串\""+str1+"\"与\""+str2+"\"的比较");
//取数组右下角的值,同样不同位置代表不同字符串的比较
System.out.println("差异步骤:"+dif[len1][len2]);
//计算相似度
float similarity =1 - (float) dif[len1][len2] / Math.max(str1.length(), str2.length());
System.out.println("相似度:"+similarity);
}
//得到最小值
private static int min(int... is) {
int min = Integer.MAX_VALUE;
for (int i : is) {
if (min > i) {
min = i;
}
}
return min;
}
}






